The Terror That Quacks in the Night: Night Flight Calls!

It has come to my (own) attention that I have of late been focusing on the more physics side. So in post I thought it would be fun to take a listen to one of the lesser known bird sounds, night flight calls.

Not quite what I had in mind

As an avid not-birder I found myself out of my depth and so enlisted the help of an expert; Chris Tessigila-Hymes of the Cornell Lab of Ornithology who graciously agreed to help me out. Chris is an skilled birder and fellow acoustics nut. He is also the listowner of three birding eList list serves, including one dedicated night flight calls: the NFC-L eList.  For the record, anything that sounds relatively intelligent and accurate in this post may be attributed to Chris. Any flubs are entirely the fault of the author.

Chris Tessagila-Hymes (Ornithologist extremus). Identifying features: bird-friendly coffee (for the early bird), birder t-shirt (to avoid confusion with mycologists) and beard (doubles as a bird hide and insulation)

On to the real content.

Night flight calls, Chris tells me, are used to describe the zeeps, chips, soft whistles and other calls that are produced by migrating birds. Like birdsong these calls may be used to identify species or group of species. However, night flight calls differ greatly in their structure, being only milliseconds in duration and orders of magnitude quieter than song. Moreover, where song is produced primarily by males and used as a territorial display, it is thought that both sexes produce night flight calls during the spring and fall migration and the purpose of the call is much more nuanced.

Each year 3-5 billion birds make the round trip migration to southern wintering grounds. Some birds, such as the arctic tern, travel from the arctic to the arctic to antarctic twice a year. These birds have evolved to carefully take advantage of abundant food resources at specific regions throughout their journeys. Therefore it is critical to identify and protect key habitat along the migratory routes in order to ensure the success of these species.  Unfortunately, it can be prohibitively expensive to to study migratory routes as scientists have historically been restricted to using expensive technology such as RADAR or geolocators. However, over the last few decades recording technology has become increasingly affordable, allowing both the novice and expert to gain a better understanding of the migrating birds overhead.

Chris has been recording calls for several seasons.

"Night flight calls are exiting because by listening to them it offers us an opportunity to actually hear what is going on overhead at night, which we otherwise cannot see without using advanced technologies such as with RADAR or Thermal Imaging. Over the course of a given night of migration, you can sometimes hear more individuals of a single species than you would ever otherwise see in your entire birding lifetime."

One reason small birds may migrate at night

But one wonders, why would birds chose to migrate at night when they can't see? The answers might surprise you (they did me). First, one reason may be to avoid predatory birds such as falcons which commonly take out small, migrating birds. Second, according to NOVA it is thought that some birds migrate by the stars! How freaking cool is that?

But birds that opt to migrate at night face additional challenges. Principle among these is how to keep the flock together. When vision fails, sound is often a good alternative means of communication. Night flight calls may serve as contact calls, where members call and listen for others in order to keep the flocks together. The calls could also be used to avoid mid-air collisions or allow birds to form night-migrating flocks that say together in the day to forage. Another hypothesis being considered is that some birds may use night flight calls as a rudimentary form of echolocation. During periods of low visibility, e.g. during the pre-dawn decent into forest or scrub (or central park) the echos from the calls may provide some information about their surroundings.

Given all the potential benefits of producing calls, it would make sense that all migrating birds would produce them. Not so! As you will recall, there are plenty of nighttime predators as well. Owls, most notably have amazing hearing worthy of a post of their own. This is one more reason night flight calls are generally shorter and quieter than birdsong. Interestingly, some migrating birds cheat in the game of evolution; they remain silent but form mixed flocks with species that do produce night flight calls. Bastards.

Anwyho, one of the coolest things about  night flight calls is the ease at which novices can get involved. Given his extensive experience I asked him what would be the best way to learn to identify different species of birds at night.

If you have good hearing, you don't need a super setup to listen. Pay attention to the weather and known when to step outside at night to listen. After the passage of a cold front in the fall and after the passage of a warm front in the spring (or before a cold front passes). These are the times when the wind is favorable to each migration season. Here's a useful link to a regularly updated Wind Map.

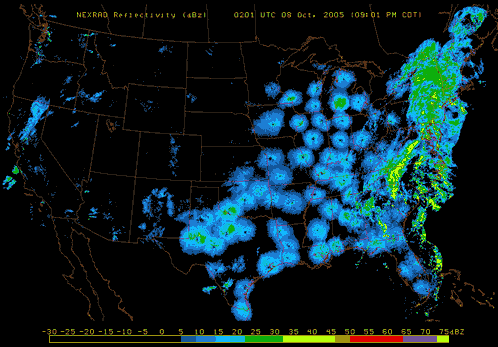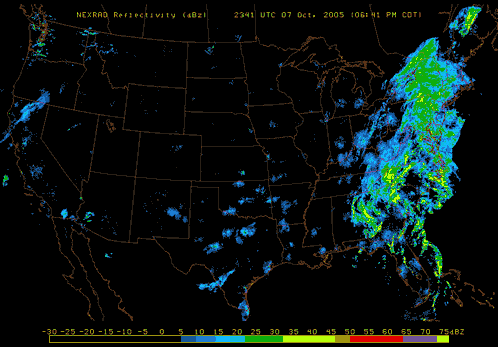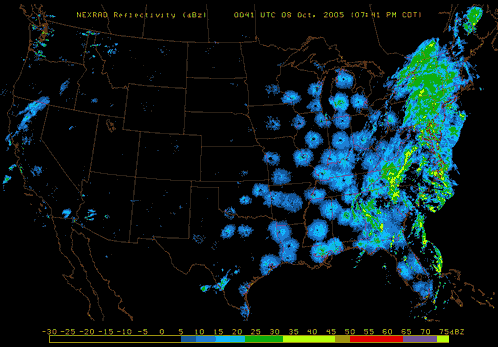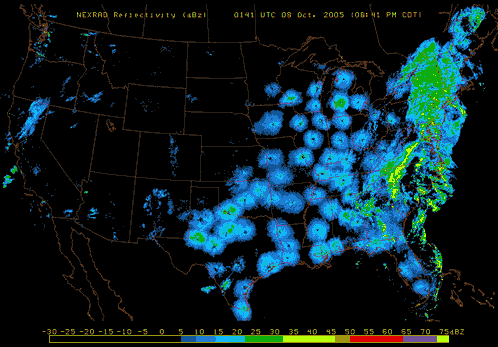
 Also, pay attention to nighttime weather by watching the reflectivity at various NEXRAD Radar stations across the United States. If you see lots of active NEXRAD Radar reflection at night near your listening site, this means birds, insects and bats are aloft! Here are a couple of NEXRAD Radar sites that are useful tools to use: NOAA National Mosaic Radar Loop and Paul Hurtado's Radar Archive.

Migrating birds seen taking off at sunset on NASA radar (http://spaceplace.nasa.gov/)

To build your own recording device Chris suggests checking out Bill Evans' website OldBird.org  where instructions are freely available. Several tools area available to analyze collected sound including Raven , Audacity, and Syrinx software. Species identification can be done by comparing recordings to those made by others, e.g. the Evans and O'Brien CD-ROM 'Flight Calls of Migratory Birds' and the night flight library. There are also several detectors on the website but I (the author) have no idea if or how they function so use at your own risk. If you want to discuss your findings with other like minded enthusiasts head over to the to the NFC-L eList. Then, once you are sure of what you've recorded enter your data into the citizen science project eBird following the night flight call reporting protocol. 

Lastly, I asked if Chris had any advice for aspiring night flight recording artists. 

Okay. If you decide to monitor night migrants with your own rooftop-mounted listening station, I highly recommend you take great care when climbing into and out of a window. During the spring of 2013, I was climbing out my window at night to service the microphone after a rainstorm. As I did this, I somehow awkwardly bent my right knee too much in a lateral direction (the way it's not supposed to bend…). The result of this movement was a perfect "bucket handle" tear of the medial meniscus cartilage in my knee. This required surgical removal of the "handle" part of the tear and effectively rendered me out of commission for the rest of the spring and summer field season that year. Though, happily, I was still quite capable of listening to night migration from my bedroom.

So, kudos to Chris to being more committed to his hobbies than I ever endeavor to be. 

Of course a big thanks to you all for reading. Finally, a special, huge, great big thanks to Mr. Chris Tessagila-Hymes for helping out, being a good sport and generally a good person. 

Happy Recording!

Don't Point That Thing At Me!

Source Directionality and Echolocation Clicks.

In my last post, I mentioned in passing how the directionality of the source might cause problems for some conservation applications of passive acoustics. Shortly thereafter one of my highly intelligent yet non-acoustician friends said to me,

"Directionality? Who-the-what now?"

So, in this post I shall clarify.

But how to go about discussing directional sound without first discussing non-directional sound... hum....tricky.

I know YouTube!!

Here are two videos showing how sound propagates in a (pseudo) homogenous medium. First from a spherical source (bulb changing size) then from a more complicated source.

2-D pressure wave  wave in a homogenous medium (kinda boring).

Link to gif source

3-D  pressure wave from a non-ideal source (awesome!!).

Things to notice about both of these.

1. The sound wave radiates symmetrically form the source (point of very large volcano)
2. The intensity of the sound is greater near the source. If you don't believe me I suggest standing next to an active volcano.
3. It doesn't matter from what angle you are hearing the blast, so long as the distance is the same, the sound will be the same (assuming the world is ideal).

Got it? Good. Now, with echolocation clicks number 3 is not applicable. Mammals that use sound to "see" their environment would waste energy by producing sound waves with equal intensity in all directions.  Instead, they point all the sound energy in front of them, the likely direction of travel. Like carrying a flashlight in the dark, to avoid smacking into a tree, it's generally advisable to point the flashlight ahead of you rather than behind.

How the sound propagates from echolocating animals, particularly dolphins, can be approximated by a piston in an infinitely rigid baffle.

Again, a who's-in-a-what now?

Let me draw you a picture:

Piston (circular plate) moving in and out of an infinitely rigid baffle (wall).

This is a piston, similar to what's in your car engine to make it move. However, instead of a chamber it's in an "infinitely rigid baffle" which is an erudite way to say a "wall" (physicists can be jerks like that). The term "baffle"  means that the sound that is radiated can't pass behind the piston through the wall. Therefore, the sound can only propagate outward in a hemisphere in front of the piston. Similar to the volcano example where where the shock wave can propagate upwards and outwards but not downwards through the water (roughly, calm yourself nit-pickers).

This is not to be confused with:

Author's interpretation of things that may be confused with a piston. A.k.a an extreme attempt to avoid working on a literature review.

So, as the piston moves in and out of the wall sound will be radiated as before. HOWEVER, the amplitude directly in front of the piston, called on-axis angle, will be much louder than the amplitude to the sides or the off axis angle.

Piston in a baffle (wall), sound in front of the piston is louder than to the sides

Finally, we have a somewhat confusing image of the sound field that's generated by the piston in a baffle. Note, the sound still radiates out symmetrically (gray line), however the amplitude changes with the angle away from the center of the piston (off axis angle).

Sound field generated by a piston in an infinitely rigid baffle. Color indicates amplitude (red high amplitude blue low amplitude) of the sound wave (gray line) radiating outward from the piston. Produced using k-wave software.

This is one adaptation bats and dolphins have evolved to optimize their effort when producing echolocation clicks. Using trained animals it's possible to make actual measurements of the sound field produced by the echolocation clicks. (Link to paper).

Jakobsen, Lasse, John M. Ratcliffe, and Annemarie Surlykke. "Convergent acoustic field of view in echolocating bats." Nature (2012).

Now that we know how to approximate the sound field produced by an echolocating animal the next question is why is this exciting to a conservationist? Because conservation scientists are, as a general rule, broke! Therefore, when we do have the tools and expertise available to do animal surveys using acoustics (determining how many animals are in an area based on how many calls are recorded) it's very important to understand what the probability of detecting those calls is. If we can make a simple model of the sound then we can then produce estimates of how far away that sound might be heard, and as important how many animals we might be missing with our detection device.

So there you are! That is one reason why a conservation biologist might give a hoot about the math behind pistons in a baffle.


Thanks for reading, feel free to leave a comment below!


Oh yes! I almost forgot. Don't point that thing at me! Please.
Or, an overly dramatic video exploring one way humans have adapted directional sound to their own devices.

---

Additional Resources/Images and Movies

Unfortunately, I have no code for this post because the one Matlab example was taken directly from the k-wave tutorial files.

Dan Russell's Acoustic Animations website.

For an in-depth look at pistons in a baffle, check out 

Great video by Oceans Initiative on echolocation of dolphins

Secret to a Sound Ocean from Oceans Initiative on Vimeo.

To learn more about this topic, check out:
http://www.oceansinitiative.org/acoustics/

To see the original research article:
http://onlinelibrary.wiley.com/doi/10.1111/acv.12076/abstract

Biological aspects of echolocation in dolphins.

Here is a very slow animation using k-wave of what that sound field would look like in the xy, yz and Z plane.

Sorry for the slow speed. Donations of faster computers gladly accepted.

2-D Tracking of Acoustic Sources from a Single Sensor

CAUTION! COGITATION IN PROCESS!
The following post will cover 2-D tracking of acoustic sources from a single acoustic sensor as suggested by Cato 1998. This concept is something that is often mentioned in theoretical instances but I have yet to see it applied. Below are my current thoughts on the matter and the issues I've run across while attempting to implement the method.

Passive acoustic monitoring is one way to  non-invasive study acoustically active animals (frogs, bats, snapping shrimp, codfish, toddlers etc.).

One of the most exciting things about passive acoustic monitoring  is the ability to track individual animals. What can be learned from acoustic tracking?

• Habitat preference
• Effects of anthropogenic (man-made) sounds
• Number of animals present
• Social affiliations (which animals spend more time together)

From a conservation standpoint, determining the total number of animals within a population is key in making management decisions and allocating limited resources (e.g. $$$). Sadly, there are not the resources to monitor the whole ocean, or even a small part of it at once. 

What is a scientist to do? As with anyone working on a limited budget, you make your data stretch by utilizing all the methods available. 

Once such way to get more out of your data is to use the first arrival and second arrivals (or the sound and it's echo) to gain meaningful information about the distance from the source to the receiver.

Using the time difference between the first arrival and second arrival as well as the difference in the relative amplitudes (volume) between the first and arrival and echo it is supposed to be possible to calculate the distance to and the depth of the caller, assuming you know how deep your recording device is. 

Adapted from Au and Hastings Principles of Marine Bioacoustics

For anyone interested here's how the math works.

Known variables:

τ- time difference of arrival between first arrival (R1) and echo (R2+R3)

D_hydrophone- How deep the hydrophone or acoustic detector is. In our case it's assumed to be on the ocean floor

I₁- Intensity of the first arrival (R1)

I₂- Intensity of the second arrival or the surface echo (R2+R3)

k-sqrt(I₁/I₂)

C- sounds speed in the water

Unknown variables: 

X-   Horizontal distance from source to hydrophone

R1- azimuthal distance from source to receiver

Dsource- Depth of the source

Assumptions:

1. The first recorded arrival is the direct path from the source to the receiver
2. The second recorded arrival is the echo from the surface
3. The surface is perfectly reflective (thought this can be modified)
4. K does not approach 1 
5. τ does not approach 0
6. The speed of sound (C) is uniform

Equations:

R1=(C*τ)/(k-1);

X=D_hydrophone-(R1.^2.*(k.^2-1))./(4*D_hydrophone);

Dsource=sqrt(R1^2-X^2);

Limitations:

Even under ideal circumstances, as below. This method has limitations. Very near the sensor and areas where k approaches 1 the equations break down. Below is an example of the errors that would be introduced if the sensor was in 8m of water. 

Range (R1) and source depth (Dsource) error at various distances from the receiver (red dot in lower left corner) 

Questions:

For the life of me I can make it work!  When real data are plugged into these equations, the output estimates are crazy (eg. sources 20m above the surface of the water, unlikely). 

I'm wondering if this may be, in part, due to the directional nature of the sounds I'm looking at. The origional author of this work, Dr. Cato (1998) used "whales" as an example when laying out this method. Believe it or not the term "whales" can be quite confusing. Was he referring to large whales only that tend to make low-frequency pseudo-omnidirectional sounds? Or was he referring to all animals in the cetacean family which includes everything from the blue whale to the tiny tiny (endangered) vaquita. Who's to say?

Interestingly, in Au and Hastings book they use dolphins, which produce highly directional sounds as an example, which suggests that it shouldn't be a problem. 

K-wave approximations:

To investigate whether the directionality of the source might be the issue I used K-wave software to model a dipole source with a reflective surface and measured the pressure at some distance away. 

The results from combining the K-wave pressure field with the above equations were less than ideal. The source position was way off.  Possibly this was due to the scale of the model, which is very tiny (violation of the assumptions) but it's impossible to parse out at the moment.

Pressure output from the sensor in the above k-wave model

Unfortunately, my current computer lacks the requisite *ahem* processing power to produce a scale model (meters rather than mm).

So, that's where things stand. It is presently unclear wither the errors I'm getting in my models are due to 

1. Violations of the assumptions
2. Directionality of the source
3. Something completely different 

If anyone has any brilliant ideas, I'm all ears. Thanks for reading!

---

Code

Matlab code for range error estimates below

function [tao, dis, r1, k, p1, p2]=simple_ray(c,hyd,dol, p, f)

%find the time difference of arrival between the first arrival and the surface

% bounce given speed of sound (c), hydrophone (x, y) and dolphin

% coordinates(x, y) and plot (binary)

if nargin <=4

    p = 0;

    alpha=0;

else

    T=8;

    D=hyd(2)

    [alpha_Db]=alpha_sea(f, T, D)

    alpha=10^(alpha_Db/20)

end

r1=sqrt((hyd(1)-dol(:,1)).^2+(hyd(2)-dol(:,2)).^2);

r2=sqrt((hyd(1)-dol(:,1)).^2+(hyd(2)+dol(:,2)).^2);

A=asin((hyd(2)-dol(:,2))./r1);

dis=r1.*cos(A);

tao=(r2-r1)/c;

p1=1./(r1);

p2=1./(r2);

k=r2./r1;

end

-------------------------------------------------------------------------------

function [r, x ,ds]=source_range(k, tao, dh)

% range from signal to receiver using single hydrophone and 1 surface

% reflection

% k -   Pressure ratio in pascals of the second and first arrival (P1/P2)

% tao-  Time difference between first and second arrival

% dh-   depth of hydrophone

c=1500;

r=(c*tao)./(k-1);

x=dh-(r.^2.*(k.^2-1))./(4*dh);

ds=sqrt(r.^2-x.^2);

end

--------------------------------------------------------------------------------------

%% Script used to  run above functions 

clear all; clc

c=1500;

hyd=[0 10]; % Hydrophone locations 

p=1; % Yes, make the figures

% make 1m by 1m grid

hab=zeros(hyd(2),50);

x=0:size(hab,2)-1;

y=0:size(hab,1)-1;

% Create a structure to store the k (p1/p2), tao, real horizontal distances, real horizontal ranges, range error (real-est range), and distance error

Trcking_mdl=struct('k_mask', hab, 'tao', hab, 'real_x', hab, 'rng', hab, 'rng_error', hab, 'dis_error', hab );

for ii=1:length(x)

     dol_x=ones(1,length(y))*(ii-1);

     dol_y=y;

     dol=[dol_x' dol_y'];

      % Call the simple ray function to get real horizontal distance, time difference of arrival (tao) and k (p1/p2) with input variables of speed of sound (c), hydrophone location (hyd), source/dolphin location (dol) and binary about whether to kick back figures (p)

     [tao, dis, r_true, k]=simple_ray(c,hyd,dol, p);

      % Fill in the the tracking model structure

     Trcking_mdl.rng(:,ii)=r_true;

     Trcking_mdl.k_mask(:,ii)=k;

     Trcking_mdl.real_x(:,ii)=dis;

     Trcking_mdl.tao(:,ii)=tao;

      % With known tao, k calculate the estimated range (r), horizontal distance (x_est) and source depth estimate (ds_est) using Cato 1998 method

     [r, x_est ,ds_est]=source_range(k, tao, hyd(2));

     % Calculate the error between the true range and the range obtained by Catos' method

     Trcking_mdl.rng_error(:,ii)=abs(r-r_true);

   
     % Calculate the horizontal distance error by taking the distance between the known source distances and the source distance obatined by Cato's method

     Trcking_mdl.dis_error(:,ii)=abs(dis-ds_est);

end

 %  Make some pictures!

figure (1)

subplot(2,1,1)

hold on

contourf(flipud(Trcking_mdl.rng_error), 20)

scatter(1,1, 'r', 'filled')

colormap (flipud(hot))

colorbar('EastOutside')

xlabel('Distance [m]')

ylabel('Depth [m]')

title('Range Error')

subplot(2,1,2)

hold on

contourf(flipud(abs(Trcking_mdl.dis_error)), 20)

scatter(1,1, 'r', 'filled')

colorbar('EastOutside')

xlabel('Distance [m]')

ylabel('Depth [m]')

title('Horizontal Distance Error')

figure(2)

subplot(2,1,1)

hold on

contourf(flipud(abs(Trcking_mdl.k_mask)), 20)

scatter(1,1, 'r', 'filled')

colorbar('EastOutside')

xlabel('Distance [m]')

ylabel('Depth [m]')

title('K (P1/P2)')

subplot(2,1,2)

hold on

contourf(flipud(abs(Trcking_mdl.tao)), 20)

scatter(1,1, 'r', 'filled')

colorbar('EastOutside')

xlabel('Distance [m]')

ylabel('Depth [m]')

title('Tao (sec)')

More Pictures With Sound

Couldn't resist. I did it with another picture. Enjoy.

Sound-o-gram

The Sound of Happiness

Or fun with spectrograms. 

What does happiness sound like?

Humans are primarily visual animals. As such, when processing large volumes of sound data, we often turn them into visual representations. One of the most popular ways to do this is to create a spectrogram. 

Spect-as in the frequency spectrum

Gram- drawing 

This is a spectrogram from a Raven demo file of a bird call. The wavform is at the top where time is the x axis and amplitude is the y-axis. In the bottom window amplitude is now represented by color (darker is louder), time is the x-axis and frequency is the y-axis with lower frequencies (elephant/blue whale calls being towards the bottom) and higher frequencies (bird chirps, me when startled by cold water are at the top).

Usually the standard way to teach this topic is to show how any given sound can be turned into an image using a complex set of mathematical equations (or by typing 'fft' into matlab). However, I thought it would be fun (for me at least) to look at it the other way around. What if we had an image, and wanted to turn it into a sound file.

Say we have a silly drawing and we want to turn it into a spectrogram. How would we go about that?

Fortunately, dear reader, I happen to have such silly drawing (artfully created using MS paint).

  

Silly drawing.

Now, instead of an image we are going to make an audio-representation of the drawing where time is going to be on the x-axis, frequency is going to be on the y-axis. 

First we load this image into MATLAB and turn it into a matrix with darkness values for each cell.

 The image turned into a cell matrix

Now we make a spetrum of each column (see below). A spectrum has both magnitude (volume) and phase information embedded in it. What is phase do you ask? Phase can be thought of as where on the a sin wave does our signal start? So for each frequency amplitude (dark spot) we need to know two things. 1. What is the frequency and 2. Where (from 0-2pi) does the signal start?

Spectrum (upper image) values for the slice of the happy face representing the left cheek and a bit of the squidgie hair. 

Dude! That spectrum looks weird! Why is it duplicated on the right and left half? Good catch kind sir/madam. It's duplicated because, simply put, the phase information needs a place to go. So that's where it goes. We need to duplicate the whole figure in the negative space to preserve (create) some phase information. For this process, I've gone ahead and assigned every positive value (where it's dark) a random phase from 0 to 2pi. 

The image after we've added the negative amplitude and phase bits.

Creepy no? 

Ok, so where are we? We've got our image, we've got the full spectrum (with amplitude and phase) for all our frequency values. We know how to create spectrums for each column of our image (hint, in involves typing fft into matlab).

Now, we need to transform those frequency values into time values using, imaginatively, the Inverse fft (hint: ifft in Matlab).

We do that for every column in our image and combine all the sound values and *poof* we have the sound of happiness. Or a silly picture that says "happy". 

Raven screenshot of waveform and spectrogram view of happy image. Note the vertical lines are because there is a goof in the phase for each of the spectrums. 

Thanks for hanging in there. This is what happiness sounds like!

Update 

Thought I would include the MATLAB code (warts and all) in case anyone wanted to play with it. I appologize in advance to anyone with a knowledge of DSP for the cringe-worth mistakes .

_______________________________________________________________________________

close all; clear all; clc;

%% Read in happy image

Raw_pic = imread('C:\Users\Desktop\Pamguard Tutorial Figs\Happy'. 'JPEG');

%% Turn it into a spectrogram

% Create the magnitude and add random phase

Happy_pic_mag=300.^-((im2double(Raw_pic(:,:,1)))-1); % Magnitude. Exponentially transforming to emphasize amplitude differences

Happy_pic_mag=Happy_pic_mag-min(min(Happy_pic_mag));

Happy_pic_phase=exp(rand(size(Happy_pic_mag))*2*pi*i);% Phase

% (I know, it's not quite right corrections gladly accepted)

Happy_pic=Happy_pic_mag.*Happy_pic_phase; % Magnitude and phase

% Now, set the phase of the first and last values to 1, because a very

% smart and compassionate man said so.

% 

Happy_pic(1,:)=0; Happy_pic(end,:)=0;

% Now we need to create the complex conjugate for the second half of the

% spectrogram

Happy_pic_conj=conj(Happy_pic);

Happy_spect=[flipud(Happy_pic);Happy_pic_conj];

image(abs(Happy_spect));

%% For each column in the image create the wavform

% Pick the sample parameters

fs=8000;

freqs_init=linspace(1,fs,size(Happy_spect,1));

freqs_final=[1:fs];

% I've picked the range of 0-40khz because human hearing is roughly 0-20khz

% so our nyquist frequency (fs/2) is at the top of the human range. Later reduced to 8000 because otherwise it was too squeelie

dt=1/fs; % time resolution

df=round(freqs_init(2)-freqs_init(1)); % frequency resolution

T=1/df; % Duration of each spectrogram slice

N=T/dt; % Number of points in each spectrogram slice

% Pick and overlap value

ovpl=0.01;

ovlp_pts=floor(ovpl*N/2);

% Now, scroll through each column and create the wavform

yy=[];

for ii=1:size(Happy_spect,2);

    

    Xm_raw=Happy_spect(:,ii); % Raw spectrum

     Xm=Xm_raw;

     xn=ifft(Xm)*N*df;

    

    if ii==1

    yy_start=1;

    else    

    % create start and stop points

    yy_start=((ii-1)*N)-ovlp_pts+1;

    end

    

    yy_end=yy_start+N-1;

    

    

    yy(yy_start:yy_end)=real(xn)/1200000; % reduce the volume to remove clipping

    

end

plot(yy) % idiot check

% Write the Wavfile

audiowrite('temp.wav',yy,fs); 

____________________________________________________________________________